WILL Part I: Relational Geometry

What is This Page?

This page transparently demonstrates how the laws of Special and General Relativity inevitably arise from a single principle of reduction, pure logic, and geometry. By revealing their fundamental essence, it offers elegant solutions to many long-standing problems in physics. Through simple and clear numerical calculations of well-known phenomena, this narrative will show not only that the Universe is, at its core, incredibly elegant and simple, but also that fundamental physics is accessible to any dedicated seeker, regardless of their level of mathematical perversion.

For full mathematical derivations:

WILL RG Papers

For unique testable predictions:

WILL RG Predictions

For questions and curiosity:

WILL RG AI

▶ Quick Glossary: Key Terms & Concepts

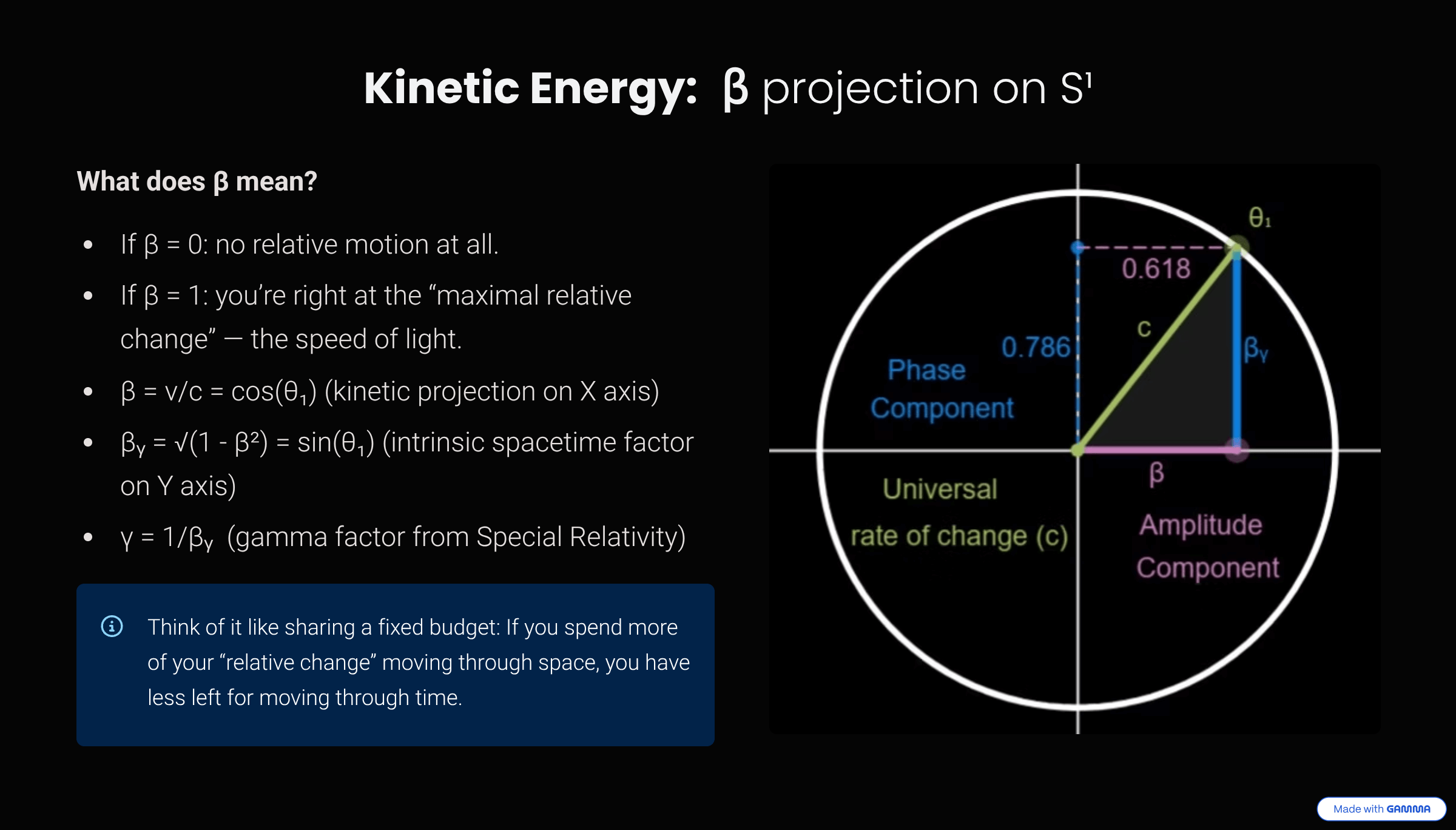
Beta (β): The kinetic projection. Representing the ratio of an object's velocity to the universal rate of change (β = v/c). It quantifies how much of the "speed of change" is perceived as motion through space relative to observer. Not an intrinsic property of an object but rather a measure of the differences between states, perceived from the perspective of an observer.

Kappa (κ): The potential projection. It measures how deeply an object is situated within a gravitational field, relative to an observer, and asociated with escape velocity (κ = v_e/c). It indicates proximity to an event horizon, at κ = 1 object has to move with the speed of light (c) in order to escape gravity (event horizon). Not an intrinsic property of an object but rather a measure of the differences between states, perceived from the perspective of an observer.

Universal rate of channge (c): Another name for the speed of light, viewed here as the fundamental, invariant tempo of change in the universe. It is not merely the speed of light but the constant rate at which all energetic interactions and transformations occur, speed limit for any change or information transfer.

Epistemological Hygiene: The principle of removing all unnecessary assumptions when building a theory, using only what’s logically required (nothing extraneous).

Event Horizon: The boundary around a black hole beyond which nothing can escape. (At this “point of no return,” the escape velocity equals the speed of light.)

Photon Sphere: A region near a black hole (about 1.5 times the Schwarzschild radius) where light can orbit in a circle if moving tangentially. It's an unstable orbit – light can fall in or escape if perturbed.

Critical Density: The maximum energy density that can can be packed into a given radius, dependent on central mass and the distance from it center. It increases closer to a central mass but never becomes infinite, thus preventing the formation of infinite densities (singularities).

Singularity: A point of infinite density where conventional physics breaks down. Standard GR predicts singularities (e.g. inside black holes); WILL Geometry avoids them by enforcing a finite critical density.

Energy–symmetry Law: The rule that energy differences always balance out between perspectives. If one observer sees a gain, another sees an equal loss — preventing any “free” energy or causality violations (this also ensures a universal speed limit).

WILL: Relational Geometry - How to Construct Reality out of One Principle

This page explores a foundational model of physics built from a single principle. Instead of describing observed phenomena with external laws, it generates the laws of physics as an inevitable consequence of that principle.

Methodological Pillars: Epistemic Hygiene, Strict Relationalism, Zero Free Parameters

To construct a theory from a single idea without introducing new postulates requires an uncompromising methodology. These pillars serve as the logical rules that guide the entire framework, ensuring no hidden assumptions or arbitrary constants are smuggled in.

Historical Breakthroughs in Physics by Deleting Separations

This approach follows a powerful historical pattern. The greatest leaps in physics have consistently come not from adding new entities, but from removing a false separation. Just as Copernicus removed the Earth/cosmos divide and Einstein unified space and time, this framework targets the final, unexamined split in modern physics.

The False Separation Between Structure and Dynamics

The contemporary split is between the structure of the universe (a fixed stage, or manifold) and the dynamics that unfold upon it (fields and energy). This separation is not an empirical discovery but an implicit assumption—an "unpaid ontological debt". By removing it, we are forced to identify geometry and energy as two aspects of a single entity.

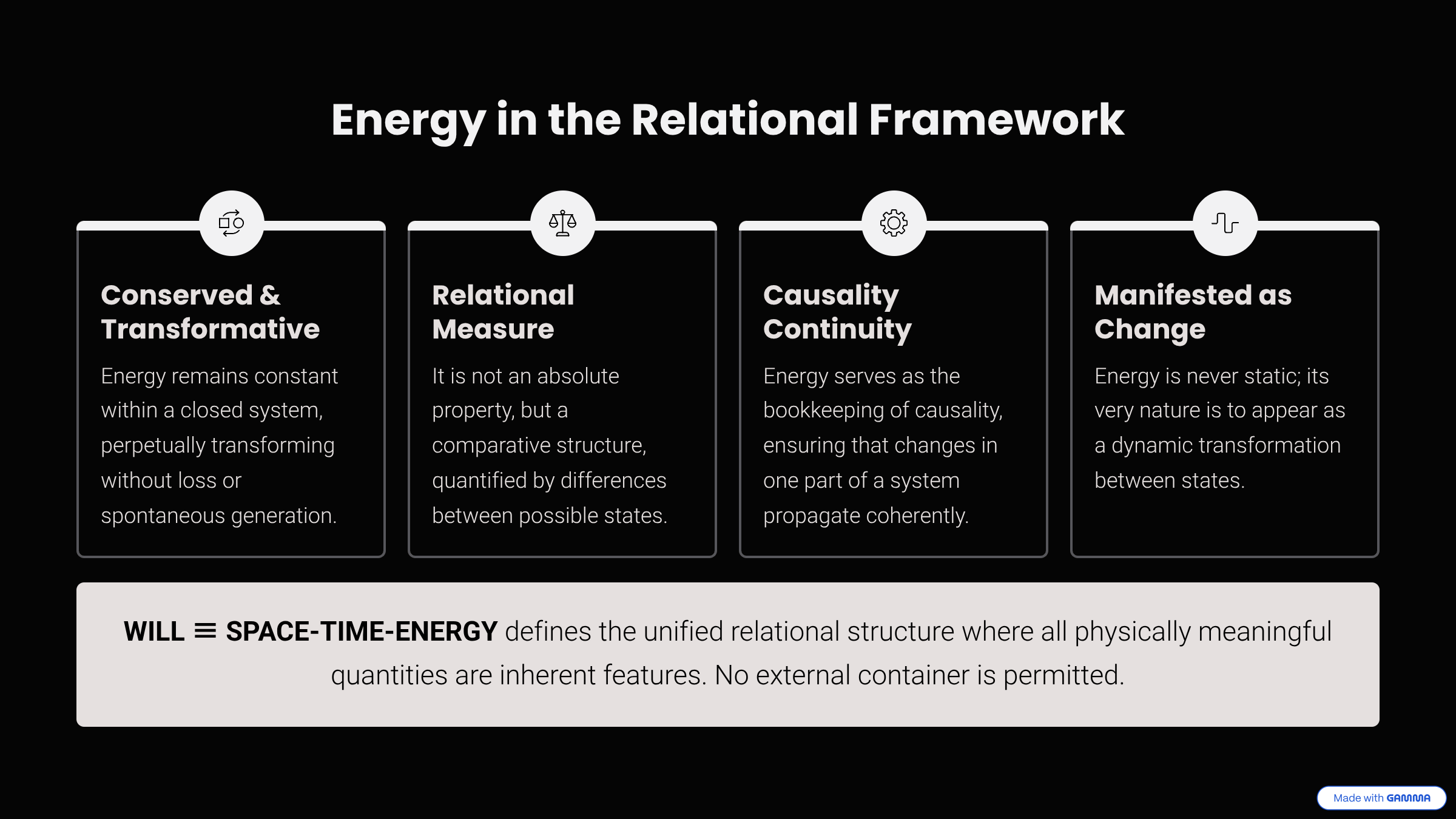
Defining Energy as Conserved, Relational, Causal, and Manifested as Change

Energy is the relational measure of difference between possible states, conserved in any closed whole. It is not an intrinsic property of an object, but comparative structure between states (and observers), always manifesting as transformation.

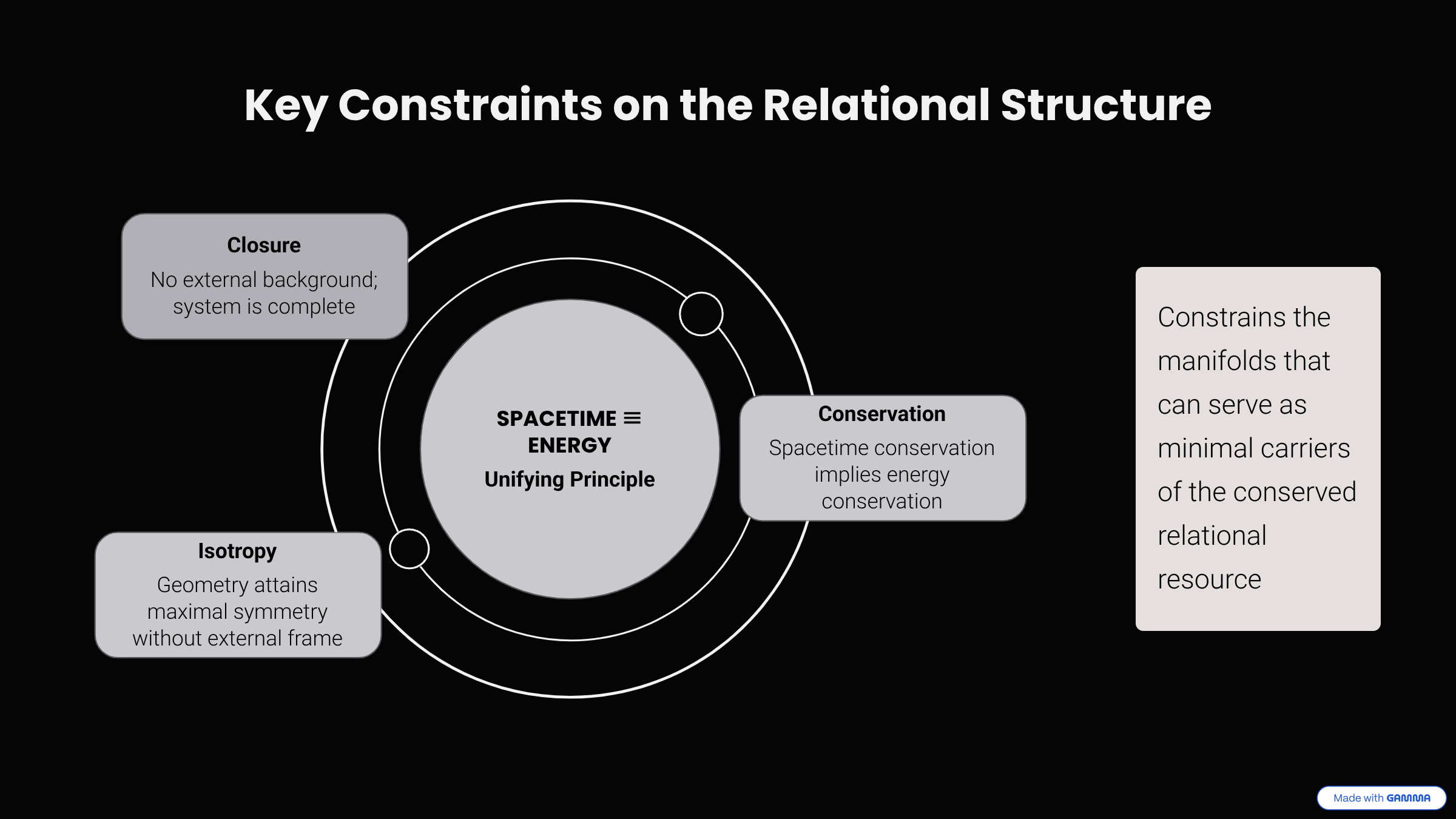
Key Constraints from the Unifying Principle: Closure, Conservation, Isotropy

These three constraints—Closure, Conservation, and Isotropy—are immediate, unavoidable consequences of a universe built from a single, self-contained principle. The next crucial question is: what mathematical forms can possibly satisfy all these rigid requirements at once?

The Circle (S¹) for Directional relations and the Sphere (S²) for Omnidirectional relations

Lemma: Closure

Under Principle 4.1 ($\text{SPACETIME} \equiv \text{ENERGY}$), WILL is self-contained: there is no external reservoir into or from which the relational resource can flow.

Lemma: Conservation

Within WILL, the total relational "transformation resource" (energy) is conserved.

Lemma: Isotropy from Background-Free Relationality

If no external background is allowed, then no direction can be a priori privileged. Thus the admissible relational geometry of WILL must be maximally symmetric.

Theorem: Minimal Relational Carriers of the Conserved Resource

The only closed, maximally symmetric manifolds that can serve as minimal carriers of the conserved relational resource are:

$S^1$ for directional (one-degree-of-freedom) relational transformation;
$S^2$ for omnidirectional (central, all-directions-equivalent) relational transformation.

S¹ and S² are not spacetime geometries, but relational manifolds.

Diagram of the Beta projection on the S¹ unit circle

--- ---

The Duality of Transformation

Lemma: Duality of Evolution

The identification of spacetime with energy and its transformations necessitates two complementary relational measures:

the extent of transformation (external displacement), and
the sequence of transformation (internal order).

Proof

Any complete description of transformation must specify both what changes and how that change is internally ordered. A single measure cannot capture both. The circle $S^1$ provides the minimal geometry enforcing such complementarity: its orthogonal projections furnish precisely two non-redundant coordinates.

We define these orthogonal projections as follows:

The Amplitude Component ($\beta$): This projection represents the relational measure between the system and the observer. It corresponds to the extent of transformation, which manifests physically as momentum.
The Phase Component ($\beta_Y$): This projection represents the internal structure of a system. It governs the intrinsic scale of its proper space and proper time units, corresponding to the sequence of its transformation. A value of $\beta_Y=1$ represents a complete and undisturbed manifestation of this internal structure, a state we identify as rest.

Conservation Law of Relational Transformation

Theorem: Conservation Law of Relational Transformation

The orthogonal components of transformation ($\beta,\beta_Y$) are bound by the closure relation:

$\beta^2 + \beta_Y^2 = 1$

Proof

Since $S^1$ is closed, every point on the circle is constrained by the Pythagorean identity of its projections. Thus no state can exceed or fall short of the finite relational "budget." This closure enforces conservation across all processes.

Consequence: Relativistic Effects

Proposition: Physical Interpretation: Relativistic Effects

The conservation law implies that any redistribution between the orthogonal components ($\beta,\beta_Y$) manifests physically as the relativistic effects of time dilation and length contraction.

Proof

The components satisfy $\beta^2 + \beta_Y^2 = 1$. An increase in the relational displacement $\beta$ enforces a decrease in the internal measure $\beta_Y$. This reduction of $\beta_Y$ corresponds to dilation of proper time and contraction of proper length, while the growth of $\beta$ represents momentum. Thus the relativistic trade-off is the direct physical expression of the geometric closure of $S^1$.

The geometry of spacetime is the shadow cast by the geometry of relations.

Energy Momentum Identity on the S¹ Circle

--- ---

Kinetic Energy Projection on $S^1$

Since $S^{1}$ encodes one-dimensional displacement, the total energy $E$ of the system must project consistently onto both axes:

$E_{X} = E \beta_{X}, \qquad E_{Y} = E \beta_{Y}$

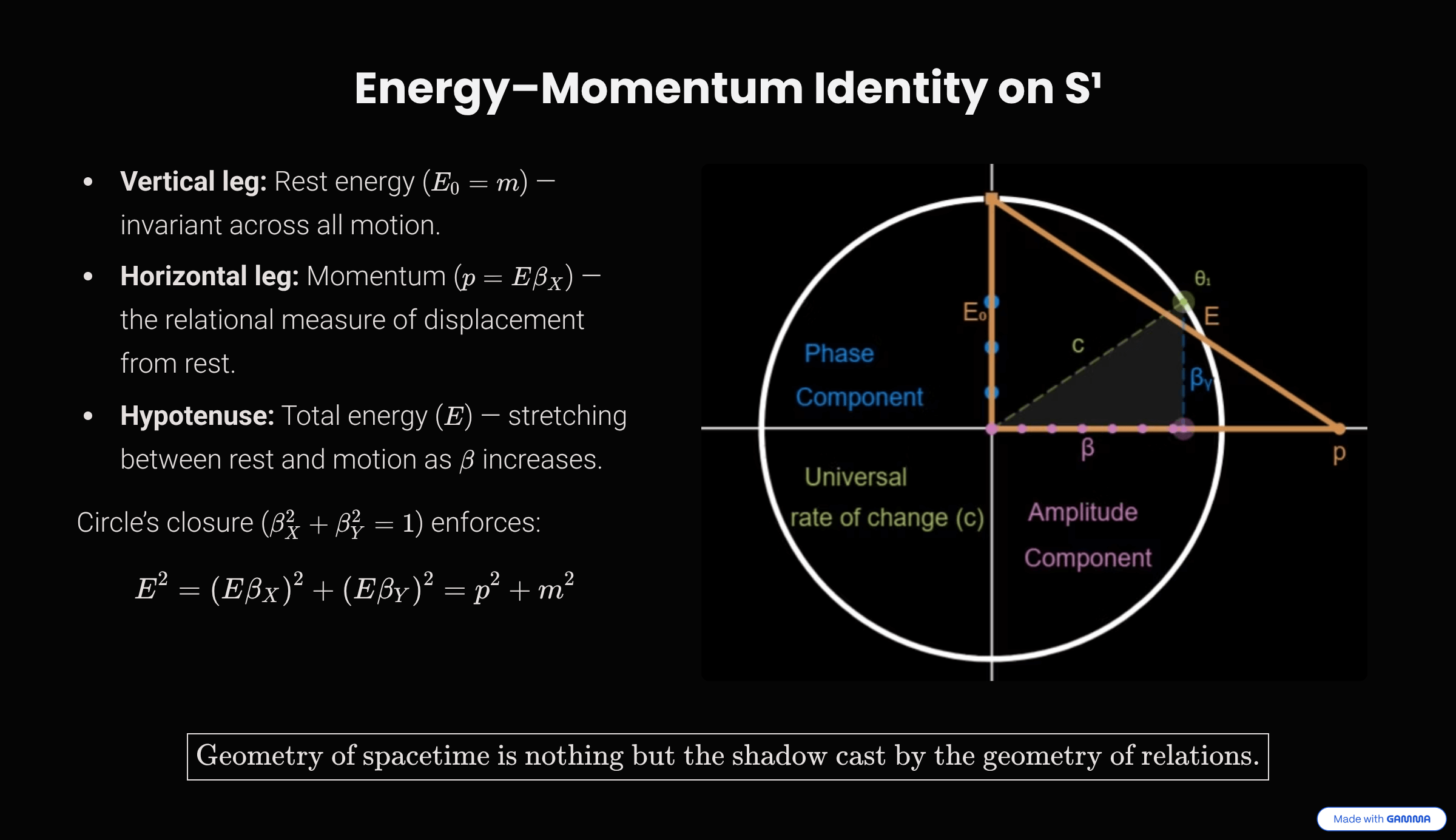
Theorem: Invariant Projection of Rest Energy

For any state ($\beta, \beta_Y$) on the relational circle, the vertical projection of the total energy is invariant:

$E \beta_Y = E_0$

Proof

When $\beta=0$, closure enforces $\beta_Y=1$, yielding $E=E_0$. Since closure applies for all $\theta_1$, the vertical projection $E\beta_Y$ remains equal to this rest value in every state.

Corollary: Total Energy Relation

From the theorem it follows that:

$E = \frac{E_0}{\beta_Y} = \frac{E_0}{\sqrt{1-\beta^2}}$

The historical Lorentz factor is the reciprocal of $\beta_Y$: $\gamma$ = 1/$\beta_Y$.

Rest Energy and Mass Equivalence

Corollary: Rest Energy and Mass Equivalence

Within the normalization $c=1$, the invariant rest energy equals mass:

$E_{0} = m$

Proof

From the invariant projection $E\beta_Y = E_0$ and closure of $S^1$, no additional scaling parameter is required. Hence the conventional bookkeeping identities $E_0 = mc^2$ or $m = E_0/c^2$ reduce to tautologies. Mass is therefore not independent, but the rest-energy invariant itself.

Mass is the invariant projection of total rest energy.

Energy–Momentum Relation

Proposition: Horizontal Projection as Momentum

On the relational circle, the unique relational measure of displacement from rest is the horizontal projection $E\beta$; hence:

$p \equiv E\beta \quad (c=1)$

Corollary: Energy–Momentum Relation

With $p$ identified by the proposition and $m=E_0$, the closure identity yields:

$E^{2} = p^{2} + m^{2} \quad (c=1)$

Equivalently, upon restoring $c$:

$E^{2} = (pc)^{2} + (mc^{2})^{2}$

Proof

By closure, $(E\beta)^2 + (E\beta_Y)^2 = E^2$. Substituting $p=E\beta$ and $m=E_0$ proves the claim. Restoring $c$ is dimensional bookkeeping: $p\mapsto pc$ and $m\mapsto mc^{2}$, while $E$ remains $E$, yielding the standard form.

The relation $E^{2}=p^{2}+m^{2}$ is the geometric identity of $S^1$.

Diagram of the Kappa projection on the S² unit sphere

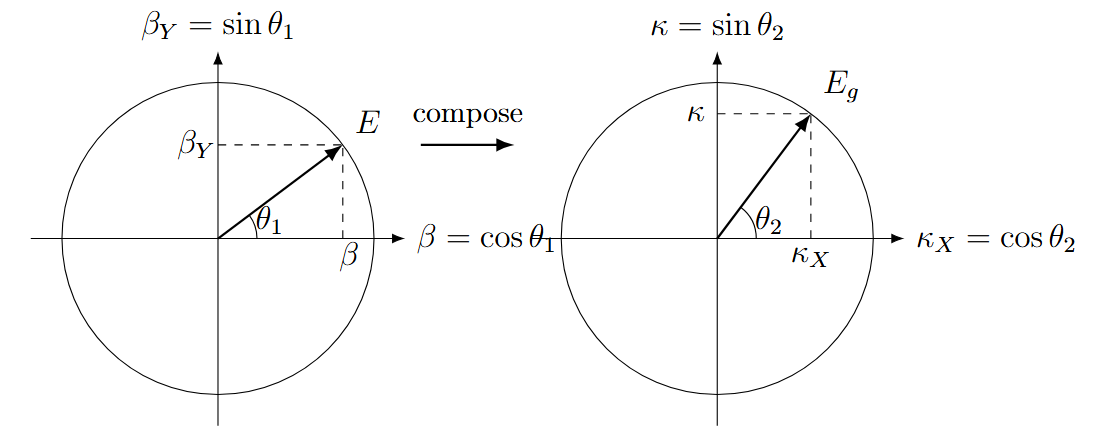
With both the kinetic (SR on $S^1$) and potential (GR on $S^2$) projections defined, we can now compose them. This composition reveals how WILL Geometry derives one of General Relativity's core postulates—the Equivalence Principle—not as an axiom, but as a structural necessity.

Clear Relational Symmetry Between Projections

$\beta=\beta_X, \quad \kappa=\kappa_Y, \quad \theta_1= \arccos(\beta), \quad \theta_2 = \arcsin(\kappa)$ $\kappa^2 = 2\beta^2$
Algebraic Form	Trigonometric Form
$1/\beta_Y= \frac{1}{\sqrt{1-\beta^2}}$	$1/\sin(\theta_1) = 1/\sin(\arccos(\beta))$
$1/\kappa_X = \frac{1}{\sqrt{1-\kappa^2}}$	$1/\cos(\theta_2) = 1/\cos(\arcsin(\kappa))$
$\beta_Y = \sqrt{1-\beta^2}$	$\sin(\theta_1) = \sin(\arccos(\beta))$
$\kappa_X = \sqrt{1-\kappa^2}$	$\cos(\theta_2) = \cos(\arcsin(\kappa))$
$p=E_0\beta/\beta_Y$	$p=E_0\cot(\theta_1)$
$p_g=E_0\kappa/\kappa_X$	$p_g=E_0 \tan(\theta_2)$

The Combined Energy Parameter $Q$

The total energy projection parameter unifies both aspects, describing the combined effects of relativity and gravity.

$Q = \sqrt{\kappa^2 + \beta^2}$

$Q^{2} = 3\beta^2 = \frac{3}{2}\kappa^2 = \frac{3R_s}{2r}$

$Q_t = \sqrt{1-Q^2} = \sqrt{1-3\beta^2} = \sqrt{1-\frac{3}{2}\kappa^2}$

$Q_r = \frac{1}{Q_t}$

Relativistic ($\beta$) and gravitational ($\kappa$) modes are dual aspects of one energy-transformation constraint.

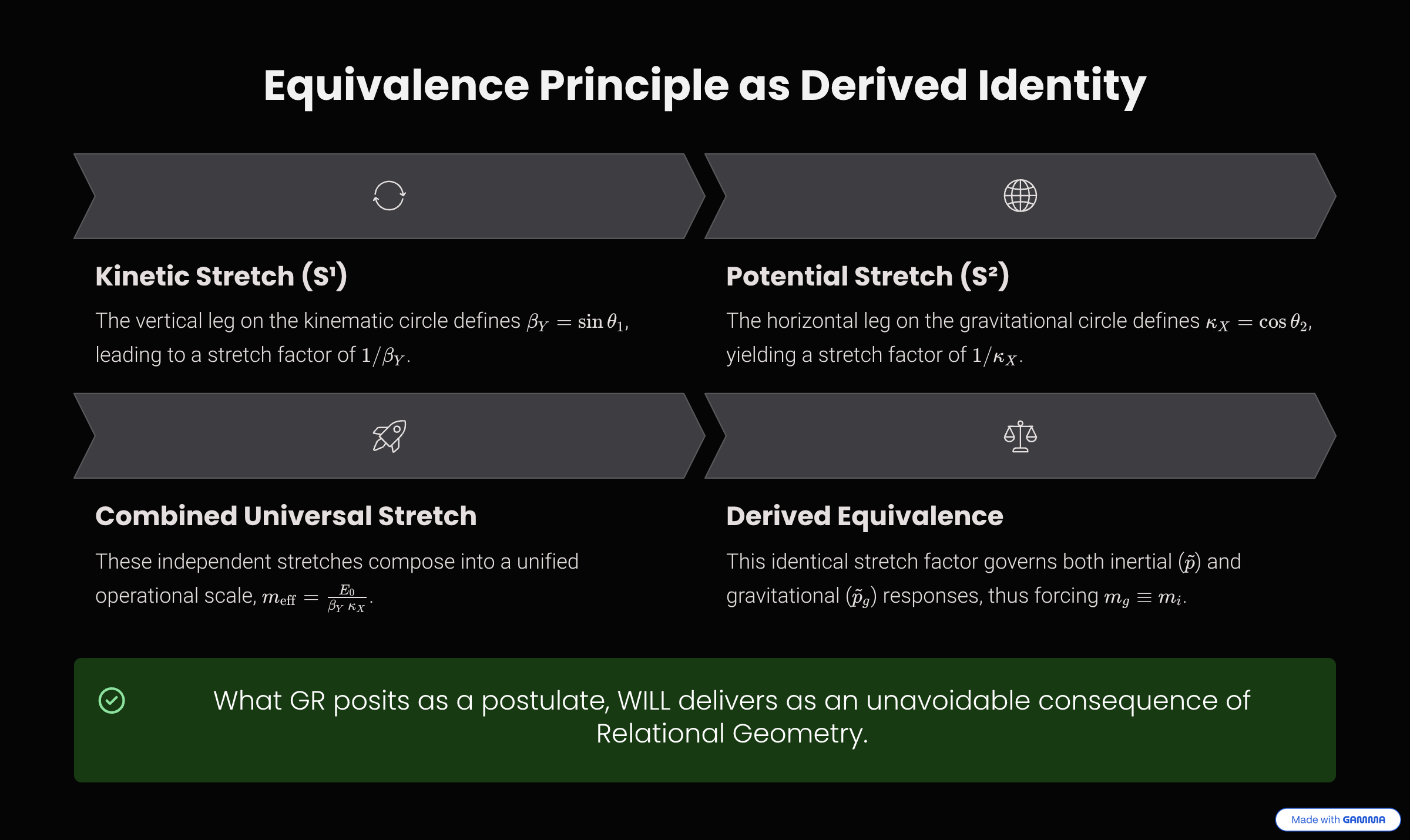
Equivalence Principle as a Derived Identity

In General Relativity, the Einstein Equivalence Principle is introduced as an independent postulate: $m_g \equiv m_i$. Within WILL Geometry, no such axiom is required.

Composing the independent stretches from the kinematic ($1/\beta_Y$) and gravitational ($1/\kappa_X$) projections gives the total local energy:

$E_{\text{loc}} = \frac{E_0}{\beta_Y \cdot \kappa_X} = \frac{E_0}{\sqrt{(1-\beta^2)(1-\kappa^2)}}$

The inertial ($\tilde p$) and gravitational ($\tilde p_g$) projections share the same operational scale, governed by an identical effective mass factor, $m_{\text{eff}}$. Hence, the equality is not assumed but is forced by the structure:

$m_g \equiv m_i = m_{\text{eff}}$

Remark on Eötvös-type precision

In WILL, the only invariant is $E_0$, and the effective response is the universal stretch factor $1/(\beta_Y\kappa_X)$. Since this factor depends solely on geometry and not on the composition of the test body, the universality of free fall follows by construction. What GR postulates, WILL reproduces as structural necessity.

What GR posits as a postulate, WILL delivers as an unavoidable consequence.

This derived equivalence is a profound consequence of composing the two projections. The framework's consistency, however, demands an even deeper connection: a precise 'exchange rate' that must exist between the kinetic and potential modes themselves.

The topological ratio of S² to S¹ resulting in k²/β² = 2

Unification of Projections: The Geometric Exchange Rate

The Principle of a unified relational resource (Energy) requires a self-consistent "exchange rate" between its kinetic and potential modes. This rate is not an arbitrary parameter but is dictated by the intrinsic geometry of the relations themselves.

1. The Ratio of Relational Degrees of Freedom

An omnidirectional spherical relation ($\kappa^2$ on $S^2$) requires two degrees of freedom (2D), while a directional circular relation ($\beta^2$ on $S^1$) requires only one (1D). The intrinsic ratio is therefore 2. This is formally expressed as the ratio of their total solid angles:

$\frac{\text{Total Closure of } S^2}{\text{Total Closure of } S^1} = \frac{4\pi}{2\pi} = 2$

2. The Quadratic Nature of Energetic Realization

Energy is fundamentally quadratic in nature. The energetic significance of a state is proportional not to the amplitude of a projection ($\beta$, $\kappa$), but to its square ($\beta^2$, $\kappa^2$).

Proposition: Energetic Closure Criterion

In closed regimes, the unique quadratic balance compatible with directional ($S^1$) vs omnidirectional ($S^2$) resource splitting is:

$\kappa^2=2\beta^2$

The Principle as a Diagnostic Invariant

The relation $\kappa^2 = 2\beta^2$ holds if the system is energetically closed (e.g., circular orbits). In open systems, its violation can be used to determine the magnitude of energy flow through unaccounted-for channels. When all channels are included, the equality is restored.

Geometric Distribution ($\kappa^2$) ≡ Kinetic Distribution ($\beta^2$) × 2

This topological ratio is the fundamental 'exchange rate' for energy within any closed system. It allows us to unify both kinetic and potential projections into a single, combined vector that describes the total energetic state of an object.

Total Projection Q as a vector on the Beta-Kappa plane

The Total Projection Parameter Q

--- ---

The combined effects of the kinetic ($\beta$) and potential ($\kappa$) projections are unified into a single vector, $Q$, representing the system's total projection budget.

$Q = \sqrt{\kappa^2 + \beta^2}$

$Q^{2} = 3\beta^2 = \frac{3}{2}\kappa^2$

$Q_t = \sqrt{1-Q^2}$

This parameter describes the total energetic state of a closed system. Its boundary condition, $Q=1$, corresponds to a critical state of the system—the photon sphere, where the geometry reaches its null-circumnavigation limit.

While the $Q$ parameter describes the static geometric state of a system, transformations between states are governed by the framework's core dynamical rule: the Energy-Symmetry Law.

Energy as a Relation — What κ and β Actually Mean

Key Principle:

Energy isn’t something objects “have” — it’s a measure of differences between states.

When we drop anthropocentric distortions, a clear and intuitive picture emerges:

Physical parameters like energy, speed, and gravitational potential don’t belong to objects.
Instead, they represent how we, as observers, measure differences from our own point of view.

In this relational view, your perspective is always the reference frame. You are always at zero. Everything else is described by how it differs from your state:

β (Beta) is not an intrinsic property of a moving object. It is a measure of how much of the universal “speed of change” you see as motion through space, relative to yourself.
κ (Kappa) doesn’t describe an object’s “stored” gravitational energy. It measures how deeply an object sits in a gravitational field, as seen from your position. It’s your personal “ruler” for gravitational depth.

Think of κ and β as your own relational measuring tools:

β is how far along your “motion ruler” you project another object’s state.
κ is how deep into your “gravity well” you see another object’s state.

Energy thus emerges naturally:

Energy is simply the capacity to move between states — it’s not possessed, but relationally defined.
Saying “the object’s energy” always implicitly means “the object’s energy as measured from your perspective.”

Here’s a simple analogy:

Imagine standing on a train platform. A train passes by rapidly: to you, it has significant kinetic energy. But if you jump onto the train, it instantly becomes stationary relative to you. Its kinetic energy is now zero — because your frame of reference shifted. The energy didn’t vanish; your perspective changed.

Bottom line:

Energy, κ, and β aren’t hidden intrinsic qualities; they’re your personal, relational measurements.
All physics boils down to describing how things differ from your chosen point of view. No more, no less.

The Energy-Symmetry Law

Theorem: Energy Symmetry

The specific energy differences (per unit of rest energy) perceived by two observers for a transition between their states balance according to the Energy-Symmetry Law:

$\Delta E_{A \to B} + \Delta E_{B \to A} = 0$

Proof

Consider observer A at rest ($\beta_A=0$) on a surface with potential $\kappa_A$, and observer B in an orbit with potential $\kappa_B$ and velocity $\beta_B$. The total specific energy for the transition $A \to B$ is the sum of the change in potential and kinetic energy budgets:

$\Delta E_{A \to B} = \frac{1}{2}\left((\kappa_A^2 - \kappa_B^2) + \beta_B^2\right)$

From B's perspective, the transition $B \to A$ yields:

$\Delta E_{B \to A} = \frac{1}{2}\left((\kappa_B^2 - \kappa_A^2) - \beta_B^2\right)$

Summing these transfers gives $\Delta E_{A \to B} + \Delta E_{B \to A} = 0$. No net energy is created or destroyed in a closed cycle of transitions.

Universal Speed Limit as a Consequence

Theorem: Universal Speed Limit

The universal speed limit ($v \leq c$) emerges from the requirement of energetic symmetry.

Proof

Assume an object could exceed the speed of light, implying $\beta > 1$. The energy transfer required, $\Delta E_{A \to B}$, would become arbitrarily large. Consequently, no finite physical process could provide a balancing reverse transfer, $\Delta E_{B \to A}$, that would sum to zero. The fundamental symmetry would be broken. Therefore, the condition $\beta \leq 1$ is an intrinsic requirement for maintaining the causal and energetic consistency of the relational universe.

Single-Axis Energy Transfer and the Nature of Light

Theorem: Single-Axis Transformation Principle

For light, the kinematic projection reaches its full extent: $\beta = 1 \Rightarrow \beta_Y = 0$. All transformation of the relational energy occurs along a single orthogonal axis.

Proof

For massive systems, the energy exchange is distributed between two orthogonal projections. For light, $\beta_Y = 0$, so the complementary projection disappears. The full relational resource is realized on a single projection. Therefore, the specific energy potential for light is not halved but complete, $\Phi_\gamma = \kappa^2 c^2$, while for a massive body it remains partitioned, $\Phi_{\text{mass}} = \frac{1}{2}\kappa^2 c^2$. This explains why light experiences a geometric effect exactly twice that of a massive particle in the same field.

Causality is a built-in feature of Relational Geometry.

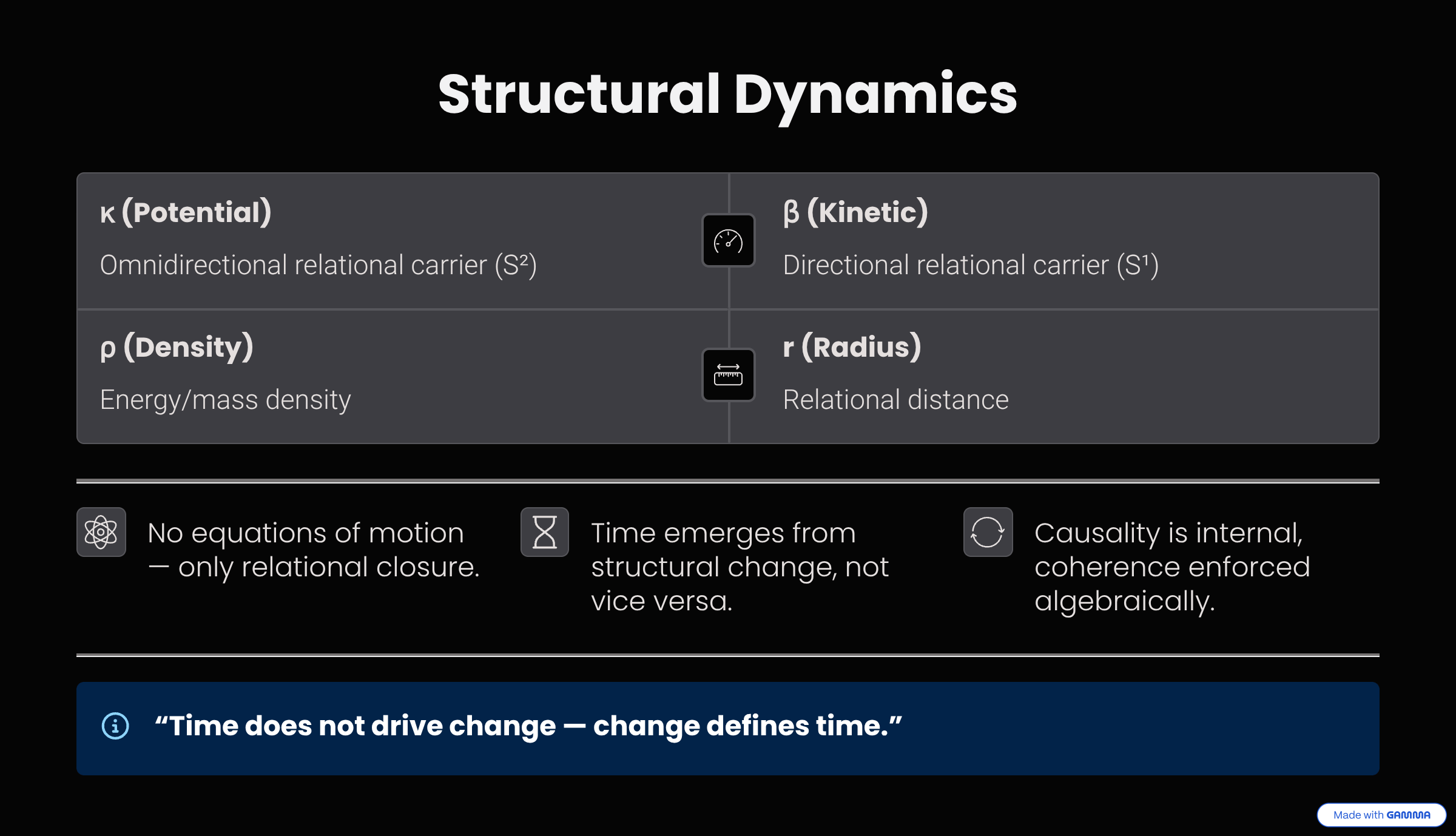
Beyond Differential Formalism: Structural Dynamics

The system is not described by differential equations of motion evolving in time. Instead, its transformation is dictated by a closed network of algebraic relations that enforce a perpetually balanced configuration. What we perceive as "dynamics" is this ordered succession of balanced states.

Time does not drive change — change defines time.

Time as an Emergent Property

In this framework, time is not a fundamental entity but a derived concept tied to changes in the system's geometry. Similar to time dilation, time intervals here are defined by the transformations of geometric parameters like $r$ and $\kappa$. A natural time scale arises from the geometry as $t_{d} = r/c$. This intrinsic time scale encapsulates the system's dynamics without invoking an independent time variable.

Algebraic Closure and Structural Causality

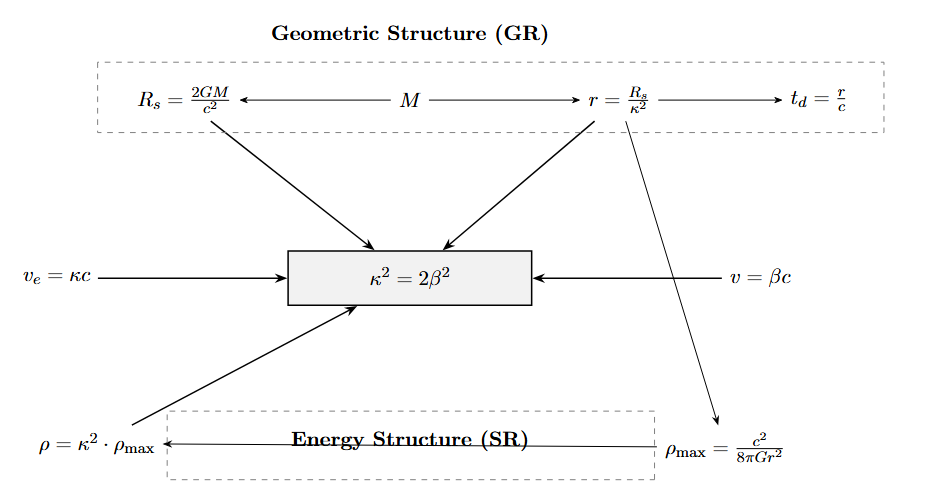
Physical dynamics emerges from a set of algebraically closed invariants. Each parameter participates in a self-consistent configuration of relational constraints. Changing any one parameter necessitates a coordinated shift in all others to maintain validity. The following set of relations expresses this minimal algebraic closure:

$\kappa^2 = 2 \beta^2$

$r \cdot \kappa^2 = R_s \quad \text{where} \quad R_s = \frac{2G m_0}{c^2}$

$\rho = \frac{\kappa^2 c^2}{8\pi Gr^2}$

$m_0 = 4\pi r^3 \cdot \rho$

Diagram of algebraic closure in WILL Geometry

Dynamics is the ordered succession of balanced configurations.

This principle of structural dynamics culminates in the framework's central equation, which unifies geometry and energy density into a single, profound statement.

In plain words: **(Gravitational depth) = (fraction of critical radius reached) = (fraction of maximum density reached)** Let’s unpack the terms: - $R_s$ is the critical radius for a given mass – essentially the Schwarzschild radius (the radius of a black hole event horizon for that mass). - $r_d$ is the distance from the center we are considering (the current radius). - $\rho$ is the energy density (including mass as energy) at that radius. - $\rho_{\max}$ is the critical density at that radius, meaning the maximum energy density that location can sustain without collapsing into a black hole. ---

The Unified Field Equation

From the energy-geometry equivalence, the complete description of gravitational phenomena reduces to a single algebraic relation. This equation expresses the core identity: the ratio of geometric scales equals the ratio of energy densities.

$\kappa^2 = \frac{R_s}{r} = \frac{\rho}{\rho_{\text{max}}}$

This single algebraic relation is the unified field equation of WILL Geometry. It ensures that curvature and energy density evolve smoothly and remain bounded, resolving the singularity problem by geometrically constraining the domain of valid projections.

No Singularities: The constraint $\kappa^2 \le 1$ naturally prevents infinite curvature.

This equation closes the theoretical loop, demonstrating that the framework's foundational principle is proven as the inevitable consequence of its own geometric consistency—a concept best visualized as the Theoretical Ouroboros.

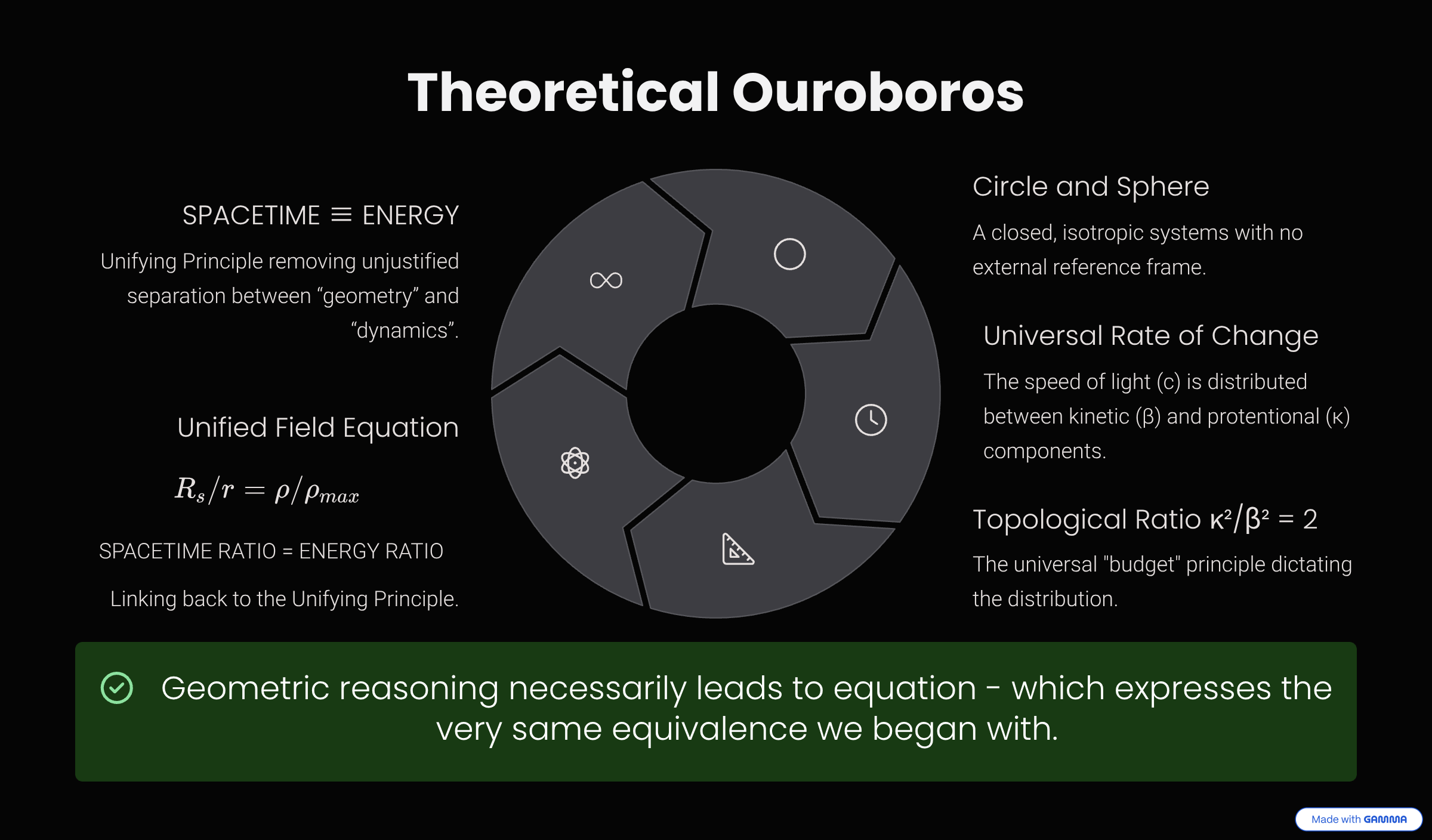
The Theoretical Ouroboros

The Unified Field Equation closes the theoretical loop. The single foundational principle, through pure geometric reasoning, necessarily leads to an equation which mathematically expresses the very same equivalence we began with.

The initial principle $\text{SPACETIME} \equiv \text{ENERGY}$ logically derives the geometry and physical laws, and these derived laws then loop back to intrinsically define and prove the self-consistency of the initial idea.

The WILL framework exhibits perfect logical closure: the fundamental principle is proven as the inevitable consequence of geometric consistency.

This logical closure is elegant, but a physical theory is only as strong as its empirical predictions. The final step is to ground this abstract framework in real-world, measurable phenomena.

Grounding the Vision in Reality

A theory born of pure logic must find its reflection in the workings of the real world. WILL Geometry passes rigorous experimental and observational tests, reproducing the successes of standard physics from deeper, more unified first principles.

Critical Orbits (ISCO & Photon Sphere)

All known GR critical surfaces emerge naturally from the geometric equilibrium of the $\beta$ and $\kappa$ projections, without solving geodesic equations.

GPS Satellites

The model correctly predicts the empirically measured time correction by unifying kinetic (SR) and gravitational (GR) effects into a single calculation.

--- ---

Mercury Precession

The theory computes the anomalous precession of Mercury’s orbit, matching the observed data with machine-level precision.

SPACETIME ≡ ENERGY: One principle defines the structure and the symmetry of reality.

The World as a Projection

This exploration is only the beginning. The model has been extended to cover cosmology and quantum mechanics, with further results and detailed applications available below. The core idea remains: energy does not exist in space—it creates space by its projection.

Documents & Results Testable Predictions Ask WILL AI Help This Research

The Name “WILL”

The name Will reflects both the harmonious unity of the equation and a subtle irony towards the anthropic principle, which often intertwines human existence with the causality of the universe. The equation stands as a testament to the universal laws of physics, transcending any anthropocentric framework.

This is not the end, but just a beginning. For the full mathematical theory, and its extensions to cosmology and quantum mechanics, see:

\(\beta=\beta_X, \quad \kappa=\kappa_Y, \quad \theta_1= \arccos(\beta), \quad \theta_2 = \arcsin(\kappa)\) \(\kappa^2 = 2\beta^2\)
Algebraic Form	Trigonometric Form
\(1/\beta_Y= \frac{1}{\sqrt{1-\beta^2}}\)	\(1/\sin(\theta_1) = 1/\sin(\arccos(\beta))\)
\(1/\kappa_X = \frac{1}{\sqrt{1-\kappa^2}}\)	\(1/\cos(\theta_2) = 1/\cos(\arcsin(\kappa))\)
\(\beta_Y = \sqrt{1-\beta^2}\)	\(\sin(\theta_1) = \sin(\arccos(\beta))\)
\(\kappa_X = \sqrt{1-\kappa^2}\)	\(\cos(\theta_2) = \cos(\arcsin(\kappa))\)
\(p=E_0\beta/\beta_Y\)	\(p=E_0\cot(\theta_1)\)
\(p_g=E_0\kappa/\kappa_X\)	\(p_g=E_0 \tan(\theta_2)\)

WILL Part I: Relational Geometry

What is This Page?

Lemma: Closure

Lemma: Conservation

Lemma: Isotropy from Background-Free Relationality

Theorem: Minimal Relational Carriers of the Conserved Resource

The Duality of Transformation

Lemma: Duality of Evolution

Proof

Conservation Law of Relational Transformation

Theorem: Conservation Law of Relational Transformation

Proof

Consequence: Relativistic Effects

Proposition: Physical Interpretation: Relativistic Effects

Proof

Kinetic Energy Projection on \(S^1\)

Theorem: Invariant Projection of Rest Energy

Proof

Corollary: Total Energy Relation

Rest Energy and Mass Equivalence

Corollary: Rest Energy and Mass Equivalence

Proof

Energy–Momentum Relation

Proposition: Horizontal Projection as Momentum

Corollary: Energy–Momentum Relation

Proof

Consequence: Gravitational Effects

Gravitational Tangent Formulation

Clear Relational Symmetry Between Projections

The Combined Energy Parameter \(Q\)

Equivalence Principle as a Derived Identity

Remark on Eötvös-type precision

Unification of Projections: The Geometric Exchange Rate

1. The Ratio of Relational Degrees of Freedom

2. The Quadratic Nature of Energetic Realization

Proposition: Energetic Closure Criterion

The Principle as a Diagnostic Invariant

The Total Projection Parameter Q

Energy as a Relation — What κ and β Actually Mean

Key Principle:

The Energy-Symmetry Law

Theorem: Energy Symmetry

Proof

Universal Speed Limit as a Consequence

Theorem: Universal Speed Limit

Proof

Single-Axis Energy Transfer and the Nature of Light

Theorem: Single-Axis Transformation Principle

Proof

Beyond Differential Formalism: Structural Dynamics

Time as an Emergent Property

Algebraic Closure and Structural Causality

Why There Are No Equations of Motion

Accretion onto a Black Hole

The Unified Field Equation

Geometric Foundation

Derivation of Energy Density (\(\rho\))

Maximal Density (\(\rho_{\text{max}}\))

The Theoretical Ouroboros

Grounding the Vision in Reality

Critical Orbits (ISCO & Photon Sphere)

GPS Satellites

Mercury Precession

The World as a Projection

The Name “WILL”